Cryptographic Security

Puzzles meet awesome spy stories as we examine methods of encryption, crack ciphers, and build a theoretical understanding of information security.

Teacher: Kit Haines

Description

Ever wanted to know how to protect a private message from prying eyes, why quantum computing allows perfectly secure bank transactions, or what the NSA can and can't actually do? Come find out the answers to these questions and more. Cryptography isn't like all that old stale math you see in high school, that has been known for hundreds of years. It is more like puzzles—often new puzzles, only two or three years old. Cryptographic security is critical to protecting sensitive information such as medical data, money transfers, and military reports, which are regularly transmitted over public channels such as the Internet or cell phone networks. There is lots of work to be done, and it is changing the world we live in rapidly.

Starting with a theoretical consideration of what "security" actually means, we will cover many protocols, from the Caesar cipher to the Advanced Encryption Standard, that have been employed to keep information secure. We will also examine systems such as Bitcoin, Kerberos, and TOR that can be built on top of powerful protocols. This class will include interactive discussions, demonstrations and activities in which students will work together to solve real-world problems.

Tentative list of topics covered

History and future of cryptography, symmetric and asymmetric encryption, encryption signatures, quantum cryptography.

For the application...

Prerequisites

Two years of high school algebra, or equivalent knowledge.

Relevant experience

Please describe any background you have in programming, contest mathematics (e.g., math league, AMC), logic, and puzzle solving (not the jigsaw kind).

Core-specific application question

You may also download these questions as a PDF.

The application question for this class consists of multiple parts. You should provide responses to all parts. These are designed to require some thought, so don’t be discouraged if it takes you a while to come up with good answers. You can do it!

Part 1. Invertible Functions

Assume the inputs to the following functions are all real numbers. Compute the inverse of the following functions or explain why no such inverse exists:

Part 2. Nogaxeh

Here we have six points (circles) on a plane arranged into a regular hexagon.

We define a move on this configuration of points, by taking any one point, and reflecting it over another point. For instance, we could take the point $$b$$, and reflect it over point $$d$$ to get the new configuration shown below:

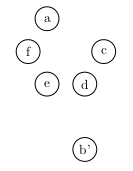
We could then take this configuration, and reflect point $$a$$ over point $$f$$ to get yet another configuration:

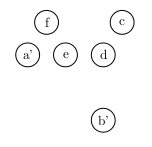
Note that each of these configurations still has six points. We delete the old location of the point each time, and we can only reflect over points that exist in the new configuration.

Can you make a larger regular hexagon: that is a hexagon with a longer side length than the original? If you can, how? If not, why not?

Part 3. Macrohard

Company Macrohard is being restructured. The company has decided to run a lottery for its one thousand employees. Each employee is equally likely to get each position. Each employee is also equally likely to get a pay rise or pay reduction (their pay definitely won't stay the same). Which of these lottery tickets are worth buying?

Ticket A costs $1 for a chance to guess the new CEO. If you guess correctly, the ticket pays you $100.

Ticket B costs $1 for a chance to guess the new board of ten directors. If you guess correctly, the ticket pays you $1,000,000,000 (yes, that is one billion dollars).

Ticket C costs $1 for a chance to guess the employees that are getting a pay raise. If you guess precisely correctly, this ticket pays you $1,000,000,000, but if you guess 80% or more correct, this ticket will still pay you $1,000,000.